Cavabı ancaq kompüter köməyiylə tapılan dünyanın ən maraqlı riyaziyyat sualı.
Riyaziyyatın sirli dünyasın tarixin hər bir dövründə insan tərəfindən tikilmiş memarlıq strukturlarında öz təsirini göstərir. Antik dövrdə istifadə edilən geometrik nümunələrin riyaziyyatı haqqında belə bir sual var ki, biz yalnız kompüterlərin köməyi ilə cavab tapa bilirik.
Bir səthdə, bitişik qabarıq beşbucaqlı istifadə edərək ən çox neçə fərqli naxış əldə edə bilərsiniz?
Biraz qarışıq oldusa, izah edək. Riyaziyyatın ən sirli formalarının beşini düşünün. Bu şəklin ağılınıza ilk gələn simmetrik formu, bu gün futbol toplarının məşhur olaraq olan naxışını təşkil edir. Simmetrik olan beşbucaqlı formasına isə bərabərtərəfli beşbucaqlı deyilir. Adından göründüyü kimi, bu forma hər tərəfə bərabərdir.
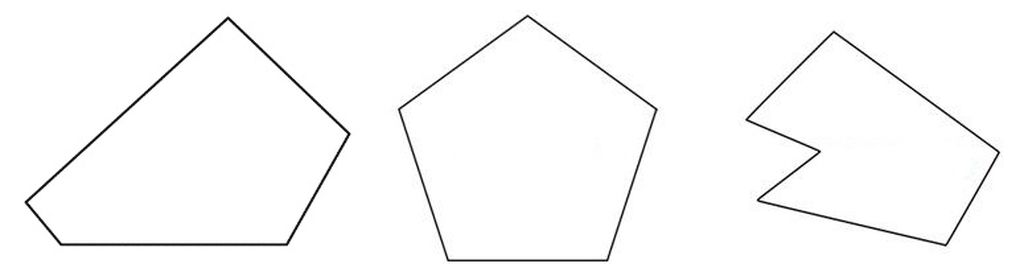
Sırası ilə; qabarıq diaqonal beşbucaqlı, qabarıq bərabərtərəfli beşbucaqlı və konkav beşbucaqlı
Bir də hər həndəsi şəkil kimi iki növ beşbucaqlı var. Bunlardan biri konkav olaraq adlandırılan və bir xarici bucağı 180 dərəcədən kiçik olan beşbucaqlıdır.Başqa sözlə, bir hissəsi şəklin içinə doğru çıxıntılıdır. Digər növü isə məşhur olaraq bildiyimiz, ümumi prinsipə uyğun olan qabarıq beşbucaqlıdır. Burada müzakirə edəcəyimiz qəhrəman da ele onun özüdür.
Bir-birinin yanında olan konveks pentagonları düzəldərək, gözə xoş gələn nümunələri yaratmaq mümkündür. Bu naxışlar, istər futbol topundakı kimi simmetrik beşbucaqlı, istər simmetrik olmayan beşbucaqlıdan meydana gəlsin, bir sərhədi vardır.
Antik dövrdən bu yana elm insanları, qabarıq beşbucaqlı neçə növ naxışda istifadə ediləcəyini maraqlanırdılar. Çünki bu gözəl şəklin arxitektura baxımdan çox tez seçim edilən 5 ayaqlı quruluşu, xüsusi işlər ortaya qoyulmasını tələb edirdi.

1985-ci ildə riyaziyyatçılar konveks pentagonları ilə tam 14 fərqli nümunə yaratmaq mümkün olduğunu söylədilər. Beləcə böyük bir maraq daha aradan qaldırılmış oldu. Ta ki 2015-ci ilə qədər. Riyaziyyatçılar Casey Mann, Jannifer McLoud-Mann və David Von Derau bu problemi həll etmək üçün Vaşinqton Universitetində işləyən bir kompüterdən istifadə etdilər. Təqdim etdikləri tezislər yeni və 15-ci ehtimalı ortaya qoyur.
Konveks pentagonlarla edilə bilən bütün nümunələr aşağıdakılardır. Başqa bir ehtimalın reallaşdırılması qeyri-mümkündür, çünki təkrara girir:

2017-ci ilə gəldiyimizdə Lyon Universitetində işləyən Michael Rao adlı bir riyaziyyatçı, inkişaf etdirdikləri kompüter proqramı sayəsində bir başqa qabarıq beşbucaqlı naxışı edilə bilməyəcəyini sübut etdi.
sh
Bir səthdə, bitişik qabarıq beşbucaqlı istifadə edərək ən çox neçə fərqli naxış əldə edə bilərsiniz?
Biraz qarışıq oldusa, izah edək. Riyaziyyatın ən sirli formalarının beşini düşünün. Bu şəklin ağılınıza ilk gələn simmetrik formu, bu gün futbol toplarının məşhur olaraq olan naxışını təşkil edir. Simmetrik olan beşbucaqlı formasına isə bərabərtərəfli beşbucaqlı deyilir. Adından göründüyü kimi, bu forma hər tərəfə bərabərdir.

Sırası ilə; qabarıq diaqonal beşbucaqlı, qabarıq bərabərtərəfli beşbucaqlı və konkav beşbucaqlı
Bir də hər həndəsi şəkil kimi iki növ beşbucaqlı var. Bunlardan biri konkav olaraq adlandırılan və bir xarici bucağı 180 dərəcədən kiçik olan beşbucaqlıdır.Başqa sözlə, bir hissəsi şəklin içinə doğru çıxıntılıdır. Digər növü isə məşhur olaraq bildiyimiz, ümumi prinsipə uyğun olan qabarıq beşbucaqlıdır. Burada müzakirə edəcəyimiz qəhrəman da ele onun özüdür.
Bir-birinin yanında olan konveks pentagonları düzəldərək, gözə xoş gələn nümunələri yaratmaq mümkündür. Bu naxışlar, istər futbol topundakı kimi simmetrik beşbucaqlı, istər simmetrik olmayan beşbucaqlıdan meydana gəlsin, bir sərhədi vardır.
Antik dövrdən bu yana elm insanları, qabarıq beşbucaqlı neçə növ naxışda istifadə ediləcəyini maraqlanırdılar. Çünki bu gözəl şəklin arxitektura baxımdan çox tez seçim edilən 5 ayaqlı quruluşu, xüsusi işlər ortaya qoyulmasını tələb edirdi.

1985-ci ildə riyaziyyatçılar konveks pentagonları ilə tam 14 fərqli nümunə yaratmaq mümkün olduğunu söylədilər. Beləcə böyük bir maraq daha aradan qaldırılmış oldu. Ta ki 2015-ci ilə qədər. Riyaziyyatçılar Casey Mann, Jannifer McLoud-Mann və David Von Derau bu problemi həll etmək üçün Vaşinqton Universitetində işləyən bir kompüterdən istifadə etdilər. Təqdim etdikləri tezislər yeni və 15-ci ehtimalı ortaya qoyur.
Konveks pentagonlarla edilə bilən bütün nümunələr aşağıdakılardır. Başqa bir ehtimalın reallaşdırılması qeyri-mümkündür, çünki təkrara girir:

2017-ci ilə gəldiyimizdə Lyon Universitetində işləyən Michael Rao adlı bir riyaziyyatçı, inkişaf etdirdikləri kompüter proqramı sayəsində bir başqa qabarıq beşbucaqlı naxışı edilə bilməyəcəyini sübut etdi.
sh